Функции одной переменной

1. Введение

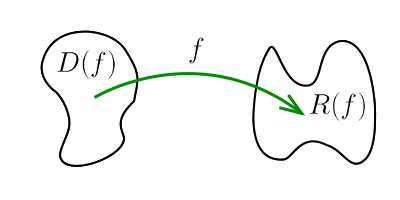
Функции — важнейшая деталь всего того внушительнейшего аппарата математической абстракции, который позволил современной высшей математике зайти так далеко. Представить себе математику без этого понятия трудно, если и вовсе возможно. Поэтому изложение в этой статье я постараюсь сделать по возможности плавным и последовательным, чтобы краеугольное понятие математического анализа не ускользнуло ни от одного читателя.

На рубеже XVIII и XIX веков во Франции жил и усердно трудился знаменитый французский математик Пьер-Симон Лаплас. Среди прочего, он считал, что то существо, которое смогло бы узнать положение и скорость всех частиц во Вселенной в какой-то один момент времени, смогло бы на основании этой информации рассчитать всю историю вселенной от начала до скончания времён. Этим он утверждал, что будущее Вселенной полностью предопределено её текущим состоянием, пусть характер связей и будет бесконечно сложным.

Мы не можем узнать состояние Вселенной с точностью до каждой частицы. Но предвидеть будущее, хотя бы в простейших вопросах, всё равно хотим. Мы хотим знать, куда поедет машина, которую мы построили, куда потечёт вода в выстроенном нами водопроводе, да вообще как будет работать любой сконструированный нами механизм. Хотя бы примерно. Хотя бы в большинстве случаев.

Здесь-то и приходит столь необходимое понятие абстракции. Мы абстрагируемся от бесконечной Вселенной, бесконечно сложно взаимодействующей с нашей шестерёнкой. Мы предполагаем, что притяжение удалённых на миллионы световых лет звёзд не сильно повлияет на воду в нашем водопроводе. Мы надеемся, что наша машина не перевернётся от подвернувшейся на дороге пылинки.

Далее. Итак, мы хотим узнать положение x{} нашей машины в каждый момент времени t на каком-то временном отрезке [0,T]. От чего оно будет зависеть? Вероятно, от начального положения машины x_0 и начальной скорости v_0. Также, вероятно, от управления u — например, от того, насколько сильно мы собираемся жать педаль газа в каждый момент времени. Но разве это всё? Оно будет зависеть от поверхности, по которой мы едем, от гравитации (она может отличаться от земной: вдруг мы собираем марсоход?) и так далее. Но мы не можем вести расчёт для всех возможных вариантов поверхности и гравитации. Здесь и приходит абстракция: мы полагаем поверхность идеально ровной, а гравитацию, например, земной; для пущей простоты отпускаем педаль газа вообще и исследуем зависимость положения x{} только от времени t. Это и будет значить, что мы определили и ищем функцию одной переменной f, представляющую из себя не что иное, как саму численную зависимость x{} от t. Такую зависимость в математике принято обозначать x=f(t).

Зависимость, ту или иную, мы можем знать или не знать, но как бы там ни было (и это ещё одна абстракция), функция — всегда «чёрный ящик», принимающий на вход одно число (и не обязательно число) и выдающий на выходе другое:
Функция - это чёрный ящик, принимающий на вход одно число и выдающий на выходе другое.
Знаем мы, что в чёрном ящике, или нет, но всегда, когда мы говорим «функция», мы подразумеваем чёрный ящик целиком, не вдаваясь в подробности его работы.

Зависимости бывают разными. Это могут быть зависимости положения от времени, объёма от температуры и так далее. Положение может измеряться в метрах, время — в секундах, температура — в градусах, допустим, по шкале Кельвина. Физики любят везде явно указывать единицы измерения, но мы будем их опускать, потому что единицы измерения нас не так волнуют и не сильно влияют на решение (ну в самом деле, от того, назовём мы метр метром или ста сантиметрами, решение задачи не изменится). Пусть, например, мы рассматриваем элементарную зависимость площади квадрата от длины его стороны: S=f(a). И площадь S, и длину стороны a мы будем считать просто вещественными числами, подразумевая, что единицы измерения или классические (метры, квадратные метры), или определены где-то далеко-далеко, в условии задачи.

Есть ещё один важный момент. Зависимость площади квадрата от длины стороны мы, конечно, знаем: S=a^2. И, теоретически, мы могли бы подставить в эту формулу на место a совершенно любое вещественное число. Но соответствует ли это логике задачи? Может ли у квадрата быть сторона отрицательной длины? Кажется, нет. Значит, мы пишем формулу S=a^2, подразумевая, что a>0. Это может показаться неважным; но функции ведь могут быть гораздо сложнее. Например, если бы у нас была зависимость вида y=\ln x, то отрицательные x{} подставлять в неё было бы уже попросту нельзя, иначе наш калькулятор или программа просто остановились бы и отказались работать дальше. А если бы мы вытворили такое при решении задачки на бумаге, то в результате могли бы получить очень неожиданные «теоретические» результаты, что-нибудь вроде 1=0. Если усложнить ещё и выражение под логарифмом, например, задать функцию вида y=\ln≤ft((1) ⁄ (2)+\cos x\right), то понять, какие x{} годятся, а какие — нет, становится ещё сложнее; в таких случаях за ответом на этот вопрос зачастую обращаются к задаче, из которой к нам пришла столь хитрая зависимость, и пытаются понять, какие возможны x{}, исходя из, например, физических соображений.

Таким образом мы подходим к одному важному определению: если дана некоторая функция f, определяющая зависимость y=f(x), то множество допустимых x{}, для которых эта зависимость определена и имеет смысл, называется областью определения функции f. Обычно оно обозначается как D(f) или \mathrm{dom} f, от английского слова domain.

Ещё одна важная вещь, которую стоит сразу же упомянуть — область значений. Областью значений функции f, определяющей зависимость y=f(x), называется множество всевозможных значений, принимаемых этой функцией на множестве D(f), то есть множество
R(f)={y | ∃ x∈ D(f):y=f(x)}.

Оно может также обозначаться как \mathrm{cod} f или \mathrm{Im} f.

Вооружившись этими двумя определениями, мы можем понять, почему функции в математике также нередко называют отображениями:
Функция как отображение D(f) в R(f)

Говорят, что функция f отображает множество D(f) во множество R(f).

Если мы теперь вернёмся к нашей образцово-показательной функции S=f(a)=a^2, то можем в наших новых терминах рассказать о ней следующее.
  1. Её областью определения является множество положительных вещественных чисел. Оно обозначется как ℝ_{+} или (0,+∞).
  2. Её областью значений также является множество положительных вещественных чисел. Этот факт, правда, неплохо было бы доказать, ведь раз мы условились, что функция — это «чёрный ящик», то если мы и можем точно знать, что ей можно пускать на вход, то что получится на выходе, да ещё и во всех возможных ситуациях — угадать не так-то просто.

    К счастью, в нашем случае всё тривиально. Достаточно заметить, что, во-первых, наша функция никогда не выдаёт отрицательные числа (и нуль), а во-вторых, что для любого заданного положительного числа S можно найти соответствующее положительное a такое, что S=a^2. Ну, здесь достаточно взять a=√{S}.

Если долго глядеть на нашу функцию, можно найти много других замечательных свойств. Например, она биективна, то есть имеет место однозначное соответствие между переменными a и S: каждому a соответствует ровно одно S и каждому S соответствует ровно одно a. Это, в свою очередь, означает, что она одновременно сюрьективна и инъективна. Но это уже совсем другая история.

Со школьной скамьи все должны иметь представление о такой функции, как синус. В школе мы учили, что синус — это отношение противолежащего катета к гипотенузе, и что это есть некоторая функция угла. Поэтому логично заключить, что областью определения синуса является множество D(\sin)=(0^{\circ},90^{\circ}) возможных углов в прямоугольном треугольнике. И, соответственно, областью значений синуса тогда является множество R(\sin)=(0,1) всевозможных соотношений катета и гипотенузы. Это несложно проверить. Ясно, что мы можем бесконечно «сплющивать» треугольник, чтобы отношение одного из катетов к гипотенузе стало сколь угодно близким к нулю, а другого — к единице. При этом сам ноль и единицу мы получить никогда не сможем.

Двигайте точку A, чтобы закрасить область определения и область значений функции \sin(α).

2. Непрерывность

Перейдём теперь к ещё одному безумно важному понятию высшей математики — непрерывности функции.

Физические процессы всегда (ну почти всегда) протекают непрерывно. Вода не может закипеть мгновенно. Сколь угодно быстро — возможно. Но не мгновенно. Она всегда пройдёт все промежуточные температуры от комнатной до 100^{\circ}. Машина не может «дёргаться» в пространстве — если она попала из пункта А в пункт Б, значит, она проехала и все промежуточные пункты.

Стало быть, если мы решили какую-нибудь физическую задачу, то первый и самый простой способ проверить верность решения — это убедиться, что рассмотренный физический процесс оказался непрерывным. Но как это сделать в математических терминах?

Умозрительно в понятии непрерывности функции нет ничего сложного. Мы говорим, что функция непрерывна, если её график нигде не рвётся. Мы говорим, что функция непрерывна в какой-то конкретной точке x_0, если её график не рвётся в этой точке. При этом ему всё ещё разрешается «переламываться», как на следующей картинке:

Главное — чтобы мы могли нарисовать график, «не отрывая карандаша от бумаги». Это важно понять: непрерывность — не то же самое, что гладкость.

Но такого определения недостаточно. Что мы будем делать, когда не будем знать заранее, как выглядит график функции? Как будем доказывать свойства произвольных непрерывных функций? К счастью, великий французский математик Огюстен Луи Коши уже решил для нас эту проблему.

Определение непрерывности функции в точке по Коши звучит так: функция f называется непрерывной в точке x_0, если для любого сколь угодно малого положительного числа ε можно подобрать такое положительное число δ, что для любой точки x, достаточно близкой к x_0, а именно такой, что |x−x_0|<δ, значение функции f в этой точке достаточно слабо отклонятся от её значения в точке x_0, а именно |f(x)−f(x_0)|<ε.

Это определение, как правило, требует некоторого умственного напряжения для понимания, но на самом деле означает ровно то, что мы говорили раньше: график функции не рвётся в точке x_0. Попробуем разобраться, почему так получается.

В определении фигурирует загадочная зависимость δ=δ(ε), индивидуальная для каждой функции в каждой точке. Давайте как-нибудь её упростим (возьмём простой частный случай) и посмотрим, что же это значит.

Ну, например, пусть δ(ε) не зависит от конкретной точки x_0 и имеет простейший вид
δ(ε)=L⋅ε, L>0,
где L — некоторая достаточно малая константа. Тогда для непрерывной функции получаем свойство
|f(x)−f(x_0)|<ε   при   |x−x_0|<L⋅ε.
А это уже можно изобразить:

То есть геометрически это условие можно интерпретировать так: если взять произвольную точку на графике функции и нарисовать вокруг неё прямоугольник размера 2Lε× 2ε, то соответствующая часть графика должна уместиться в этот прямоугольник, то есть не вылезать за его пределы вверх и вниз (хотя вправо и влево, разумеется, график имеет право продолжаться). И это должно выполняться для любого сколь угодно маленького ε.

Поскольку высота прямоугольника убывает пропорционально ε, то если где-нибудь найдётся разрыв, для него это свойство непременно окажется невыполненным:

Достаточно немножко уменьшить ε, чтобы условие перестало выполняться в точке x_0=0. И взятие константы L побольше никак на это не повлияет.

Если мы вернёмся теперь к исходному определению, охватывающему весь без ограничений набор непрерывных функций (а наше упрощённое условие, конечно же, работает не всегда: например, ломается на бесспорно непрерывной f(x)=x^2), то поймём, что и оно подразумевает то же самое. Если где-то у функции есть разрыв, то есть этакая «ступенька» высотой, скажем, h, то как только мы возьмём в нашем определении ε<h, мы уже не сможем найти подходящего δ, потому что всегда найдутся две достаточно «соседние» точки такие, что |f(x)−f(x_0)|≥ h.

Отдельным классом непрерывных функций являются так называемые липшицевы функции, важные в теории дифференциальных уравнений. Функция называется липшицевой в точке x_0, если существует некоторая достаточно большая положительная константа L такая, что
|f(x)−f(x_0)|≤ L|x−x_0|
для всех x из области определения f. Если одна и та же константа L подходит для всех точек x_0 из области определения f, то f называется просто липшицевой.

Геометрически это выглядит так: нужно подобрать константу L такую, чтобы весь (да-да, совсем весь) график функции умещался в подсвеченной на рисунке области-«бабочке» независимо от выбора её центральной точки x_0:

Видно, что при L<1 для этой функции всё плохо (график где-нибудь да выползает за рамки подсвеченной области), а при L≥ 1 — хорошо. Значит, изображённая функция липшицева с константой Липшица, равной 1. (Из рисунка ясно, что если условие выполнилось для какого-то одного L, то оно выполнится и для всех бо́льших L. Так вот, константа Липшица функции f — это наименьшее L, при котором для неё выполняется условие липшицевости во всех точках.)

Для полноты картины приведём пример непрерывной функции, не являющейся липшицевой. Это функция f(x)=√{|x|}:

Здесь, на самом деле, все точки «хорошие» — кроме нуля. Если долго увеличивать график, то можно увидеть, что при x_0=0 даже при L=100 график корня выходит за допустимые границы. Дело тут в том, что в нуле корень возрастает практически вертикально — угол между двумя симметричными ветвями на этом графике равен 0^{\circ}. Мы ещё вернёмся к этому примеру и изучим подробно этот факт, когда будем изучать производные.

Наконец, функция называется непрерывной, если она непрерывна в каждой точке своей области определения D(f).

Логичным образом можно ввести и определение непрерывности на произвольном множестве: функция f называется непрерывной на множестве X, если она непрерывна в каждой точке этого множества. Множество всех непрерывных на заданном множестве X функций обозначается C(X); соответственно, фразу «функция f непрерывна на множестве X» можно записать как f∈{}C(X). (В дальнейшем мы непременно будем так делать.)

В начале этого параграфа мы говорили о том, что непрерывность нужна нам как способ сужать круг поисков при решении физических задач, способ отсекать заведомо ложные решения. Давайте проверим это на простом примере из механики.

Опять-таки, со школы мы знаем закон равноускоренного движения материальной точки. Если в момент времени t=0 неподвижная точка начинает двигаться по прямой с ускорением a (знак которого определяет направление движения), то её положение в произвольный последующий момент времени t>0 описывается формулой
x(t)=(at^2) ⁄ (2) .
Если нарисовать график этой функции, то не возникает никаких сомнений в её непрерывности при любых значениях параметра a:

Но можем ли мы доказать факт непрерывности математически, используя определение, что подарил нам Огюстен Луи? Давайте попробуем.

Зафиксируем произвольное ускорение a. Это значит, что наше дальнейшее доказательство годится для любого a, но на протяжении доказательства a не изменяется (фиксировано!). Зафиксируем также произвольную точку t_0≥ 0. Наша задача теперь — для любого сколь угодно маленького положительного ε подобрать δ такое, чтобы при |t−t_0|<δ выполнялось
≤ft|(at^2) ⁄ (2)−(at_0^2) ⁄ (2)\right|<ε .
Выражение |t−t_0|<δ и так проще простого, поэтому давайте подробнее распишем второе, в котором есть ε.
≤ft|(at^2) ⁄ (2)−(at_0^2) ⁄ (2)\right|=(|a|) ⁄ (2) ⋅≤ft|t^2−t_0^2\right|=(|a|) ⁄ (2)⋅|t−t_0|⋅|t+t_0| .
(Все ведь помнят формулу разности квадратов, верно?)

Итак, что же мы имеем? У нас уже есть свойство
|t−t_0|<δ .
Что же касается суммы, то её можно расписать так:
|t+t_0|=|(t−t_0)+(t_0+t_0)|≤|t−t_0|+2|t_0|≤δ+2t_0 .
В первом равенстве мы просто добавили и вычли под модулем одно и то же число. (Убедитесь, что вы понимаете следующее за ним неравенство, это стандартное неравенство для модуля суммы.)

Итого исходное соотношение расписывается в виде
≤ft|(at^2) ⁄ (2)−(at_0^2) ⁄ (2)\right|≤(|a|) ⁄ (2) ⋅δ⋅(δ+2t_0) .
(2.1)
Но нам-то нужно меньше ε! Ну, что ж, на самом деле мы подобрались к ответу довольно близко: если мы теперь научимся выбирать δ=δ(ε) таким, что
(|a|) ⁄ (2) ⋅δ⋅(δ+2t_0)<ε ,
(2.2)
наша цель окажется достигнутой!

Ну а подобрать такое δ уже достаточно просто. Смотрите. Пусть δ всегда будет меньше единицы. (Скорее всего, так и будет. Мы же рассматриваем всё для маленьких ε и δ.) Тогда наше выражение (2.1) упрощается:
(|a|) ⁄ (2)⋅δ⋅(δ+2t_0)≤ (|a|) ⁄ (2)⋅δ⋅(1+2t_0) ,
и теперь достаточно подобрать δ так, чтобы вместо непонятного (2.2) выполнялось
(|a|) ⁄ (2)⋅δ⋅(1+2t_0)<ε .
А это неравенство при учёте того обстоятельства, что a и t_0 у нас фиксированные и не зависят от ε, уже простейшим образом разрешается: достаточно взять δ такое, что
δ<(2ε) ⁄ (|a|(1+2t_0)) .
Например, просто взять в два раза меньше, сократив двойку:
δ(ε)=(ε) ⁄ (|a|(1+2t_0)) .
Ну а для пущей строгости нашего доказательства возьмём
δ(ε)=\mathrm{min} ≤ft{(ε) ⁄ (|a|(1+2t_0)), 1\right} .
Мы берём этот минимум, чтобы удостовериться, что δ по-честному всегда не больше единицы, как мы предполагали ранее.

Ура!

Итак, мы получили искомую функцию δ(ε), которая обеспечивает выполнение определения непрерывности в данной точке t_0. Тут стоит обратить внимание на то, что само t_0 очень даже фигурирует в формуле этой функции в качестве постоянного параметра.

Что ж, кажется, мы убедились, что наше определение более-менее адекватно отражает суровую реальность. Функция непрерывна — значит, можно подобрать δ(ε). Непрерывна — нельзя (смотри пример в начале параграфа). Правда, подобрать δ(ε) оказалось несколько сложновато. Что же мы будем делать, если вместо скромной at^2⁄2 у нас будет функция посложнее? Что ж, тут-то и всплывёт главное достоинство строго математического определения — мы сможем доказать непрерывность многих функций, даже не обращаясь к их конкретному виду. Например, вместо того, чтобы ковыряться в ε-δ-терминологии с функцией вроде
f(x)=365x^6+31x^6+7x^5−2x^4+x ,
мы сможем просто сказать, что это сумма произведений непрерывных функций, а значит, автоматически непрерывная функция.

2.1. Арифметика непрерывных функций

Понятно, что на функциях вещественной переменной можно ввести естественную арифметику: если есть две функции f и g, логично назвать их суммой функцию s=f+g: s(x)=f(x)+g(x), разностью — функцию d=f−g: d(x)=f(x)−g(x), произведением — функцию p=f⋅ g: p(x)=f(x)⋅ g(x), частным — функцию q=(f) ⁄ (g): q(x)=(f(x)) ⁄ (g(x)). Что происходит при этом с областями определения? Вообще, обычно считается, что они у f и g совпадают. Это упрощает жизнь. Если нет — областью определения суммы, разности и произведения можно считать пересечение областей определения: ведь именно на пересечении определена и f, и g одновременно. Что же касается частного, то его областью определения считается вышеупомянутое пересечение минус множество тех точек, на которых g обращается в ноль:
D(f⁄g) = \big(D(f)∩ D(g)\big) \ { x: g(x) = 0 } .
Это позволяет избавиться от всех проблем с делением на ноль. «А? Что? Вы говорите, в этой точке деление на ноль? Да вы что, эта точка вне области определения, мы её даже не рассматриваем.»

Дальше естественный вопрос, особенно в контексте произнесённых пафосных речей про важность строгих математических определений: что будет, если нам известно, что функции f и g непрерывны? Можно ли что-то сказать о непрерывности их суммы, произведения и так далее? Оказывается, что очень даже можно. Правда, в этом параграфе нам придётся близко познакомимся с ужасающей морально неготовых студентов техникой строгих, формальных доказательств математического анализа.

Утверждение. Пусть функции f и g обе непрерывны в точке x_0. Тогда их сумма f+g тоже непременно непрерывна в этой точке.

Доказательство. Поскольку о функциях f и g нам доподлинно неизвестно ничего, кроме того, что в точке x_0 они удовлетворяют определению непрерывности по Коши, сформулированному выше, придётся нам воспользоваться именно им, чтобы исследовать функцию f+g (о которой нам известно ещё меньше).

Итак, пусть для любого ε>0 найдутся δ_f=δ_f(ε) и δ_g=δ_g(ε) такие, что
|f(x)−f(x_0)|<ε при |x−x_0|<δ_f(ε) и \hphantom{.}
|g(x)−g(x_0)|<ε при |x−x_0|<δ_g(ε).\hphantom{ и }
Раз уж мы хотим доказать непрерывность f+g в точке x_0, выпишем определение и для неё. Требуется для любого ε>0 найти такое δ_s=δ_s(ε), чтобы выполнялось
≤ft|\big(f(x)+g(x)\big)−\big(f(x_0)+g(x_0)\big)\right|<ε при |x−x_0|<δ_s(ε) .
(2.1.3)
Давайте в левой части раскроем скобки и перегруппируем слагаемые:
\begin{array}{rlcll} \big|&\hspace{−0.75em} \big(f(x)+g(x)\big) &−& \big(f(x_0)+g(x_0)\big) &\hspace{−0.75em}\big| = \\[2mm] =\big|&\hspace{−0.375em} f(x)+g(x) &−& \hspace{0.375em}f(x_0)−g(x_0)&\hspace{−0.75em}\big| \\[2mm] =\big|&\hspace{−0.75em} \big(f(x)−f(x_0)\big) &+& \big(g(x)−g(x_0)\big) &\hspace{−0.75em}\big| \end{array}
Неравенство для модуля суммы подсказывает нам, что
\begin{array}{l}\big|\big(f(x)−f(x_0)\big)+\big(g(x)−g(x_0)\big)\big| \\[4mm] \hspace{2cm}≤\big|\big(f(x)−f(x_0)\big)\big|+\big|\big(g(x)−g(x_0)\big)\big| .\end{array}
Вооружённые этим неравенством, мы готовы «угадать» ответ. Действительно, первый модуль в правой части меньше (ε) ⁄ (2) при |x−x_0|<δ_f((ε) ⁄ (2)), а второй при |x−x_0|<δ_g((ε) ⁄ (2)) — по условию задачи. Значит, остаётся взять
δ_s(ε)=\min≤ft{ δ_f≤ft((ε) ⁄ (2)\right), δ_g≤ft((ε) ⁄ (2)\right) \right} ,
чтобы оба модуля были меньше (ε) ⁄ (2) одновременно, а в сумме меньше ε.

На всякий случай проговорим итоговое доказательство. Для любого фиксированного ε>0 положим δ_s(ε)=\min{δ_f(ε⁄2),δ_g(ε⁄2)}. Тогда при |x−x_0|<δ_s(ε) справедлива цепочка неравенств
\begin{array}{rlcll} \big|&\hspace{−0.75em} \big(f(x)+g(x)\big) &−& \big(f(x_0)+g(x_0)\big) &\hspace{−0.75em}\big| = \\[2mm] =\big|&\hspace{−0.375em} f(x)+g(x) &−& \hspace{0.375em}f(x_0)−g(x_0)&\hspace{−0.75em}\big| \\[2mm] =\big|&\hspace{−0.75em} \big(f(x)−f(x_0)\big) &+& \big(g(x)−g(x_0)\big) &\hspace{−0.75em}\big| \\[2mm] ≤\big|&\hspace{−0.75em} \big(f(x)−f(x_0)\big)\big| &+& \big|\big(g(x)−g(x_0)\big) &\hspace{−0.75em}\big| \\[2mm] <\hphantom{\big|}&(ε) ⁄ (2)+(ε) ⁄ (2)=ε ; \end{array}
значит, функция f+g непрерывна в рассматриваемой точке x_0. Доказано.

С разностью читатель наверняка теперь в силах разобраться сам, а мы тем временем разберём произведение. Способ доказательства у нас будет очень похож на тот, что применялся в примере выше (про фукнцию at^2⁄2).

Утверждение. Пусть функции f и g обе непрерывны в точке x_0. Тогда их произведение f⋅ g тоже непременно непрерывно в этой точке.

Доказательство. Пусть, опять-таки, для любого ε>0 нашлись δ_f=δ_f(ε) и δ_g=δ_g(ε) такие, что
|f(x)−f(x_0)|<ε при |x−x_0|<δ_f(ε) и \hphantom{.}
|g(x)−g(x_0)|<ε при |x−x_0|<δ_g(ε).\hphantom{ и }

Выпишем условие непрерывности f⋅ g. Нужно подобрать такое δ_p=δ_p(ε), чтобы выполнялось
≤ft|f(x)⋅ g(x)−f(x_0)⋅ g(x_0)\right|<ε при |x−x_0|<δ_p(ε) .
(2.1.4)
Давайте сперва упростим себе задачу: положим g=f, то есть докажем непрерывность функции f^2 на основании непрерывности самой f. Начнём уже известным нам фокусом:
|f^2(x)−f^2(x_0)|=|f(x)−f(x_0)|⋅|f(x)+f(x_0)| .
При |x−x_0|<δ_f(ε) первая скобка сразу же меньше ε по условию теоремы, а со второй мы проведём ещё один фокус (опять-таки, в примере с параболой он был):
\begin{array}{l}|f(x)+f(x_0)|=|f(x)−f(x_0)+2f(x_0)|\\[4mm] \hspace{2cm}≤ |f(x)−f(x_0)| + 2|f(x_0)|<ε+2f(x_0) .\end{array}
Итого
|f^2(x)−f^2(x_0)|<ε⋅(ε+2f(x_0)) при |x−x_0|<δ_f(ε) .
Рассмотрим ε≤ 1. (Случаи ε>1 не особо-то нам интересны, нас по большей части интересуют сколь угодно малые величины ε. Можете попробовать на досуге привести строгое обоснование этому упрощению.) Тогда
|f^2(x)−f^2(x_0)|<ε⋅(1+2f(x_0)) при |x−x_0|≤δ_f(ε) .

Ну и, наконец, «угадаем» решение. Положим
δ_{f^2}(ε)=δ_f≤ft((ε) ⁄ (1+2f(t_0))\right) .
Тогда при |x−x_0|<δ_{f^2}(ε) выполняется неравенство
|f^2(x)−f^2(x_0)|<(ε) ⁄ (1+2f(t_0))⋅(1+2f(t_0))=ε ,
что окончательно доказывает непрерывность f^2 в точке x_0.

Что же касается f⋅ g, то тут всё становится совсем просто:
f⋅ g=(1) ⁄ (2)\Big((f+g)^2−f^2−g^2\Big)
(не поленитесь, проверьте это равенство); f^2 и g^2 непрерывны, потому что квадраты непрерывных (мы только что это доказали), f+g непрерывна согласно предыдущему утверждению про суммы, а (f+g)^2 — вместе с ней как квадрат, и, стало быть, f⋅ g непрерывна как разность непрерывных функций. Доказано.

Теперь, когда доказана непрерывность произведения непрерывных функций, непрерывность частного (f) ⁄ (g) сводится к непрерывности обратной функции (1) ⁄ (g). Утверждение будет звучать так.

Утверждение. Пусть функция g непрерывна в точке x_0 и её значение g(x_0) в этой точке отлично от нуля. Тогда функция (1) ⁄ (g) тоже непрерывна в этой точке.

(Понятное дело, что нам пришлось наложить дополнительное условие, чтобы не делить на ноль.)

Доказательство этого факта я предоставляю читателю в качестве упражнения. Обязательно проделайте его, это поможет вам раз и навсегда понять и запомнить, как устроены доказательства таких утверждений.

В качестве завершения этого параграфа подведём некоторый «дайджест» по арифметике непрерывных функций. Итак.

Пусть функции f и g непрерывны в точке x_0. Тогда:
  • их сумма f+g и разность f−g непрерывны в этой точке;
  • их квадраты f^2, g^2 и произведение f⋅ g непрерывны в этой точке;
  • если g(x_0)≠ 0, то (1) ⁄ (g) и частное (f) ⁄ (g) непрерывны в этой точке.

Соответственно, если две функции непрерывны на целом множестве (и, если нужно, функция g не обращается на этом множестве в ноль ни в одной точке), соответствующие функции будут непрерывны на всём множестве.

Как запомнить такие доказательства?
(Если вы понимаете математику и не любите болтовню, это замечание стоит пропустить.)

Весь этот формализованный кошмар действительно способен навести ужас на неподготовленного читателя (как на автора в своё время, например). Может показаться, что всё это — ненужная формальная ересь, а может — что бессистемная ерунда.

С первым проще: в нужности формализма в математике человеку, разбирающемуся в ней, сомневаться сложно. Не разбирающийся может поискать в Интернете «математические парадоксы»; впрочем, на этих страницах они тоже иногда приводятся. Есть также интересный исторический казус на эту тему. Великий Огюстен Луи Коши, которого мы здесь уже не раз упомянули и имя которого наводит страх на первокурсников матфаков, внёс, как мы можем видеть, внушительнейший вклад в формализм математики. Коши был первым, кто дал строгое определение основным понятиям математического анализа — пределу, непрерывности, производной, дифференциалу, интегралу, сходимости ряда и так далее, то бишь почти всему тому, что мы уже изучили, и многому, что мы ещё будем изучать. До него математики работали со всеми этими понятиями на интуитивном уровне. Определение сходимости по Коши и критерий Коши, о которых рассказывается в статье о последовательностях, ужасают своим формализмом, как и приведённые нами доказательства, основывающиеся на них. Однако даже Коши оказался не безупречно строг. Он считал очевидным один факт, который требует непростого доказательства, и опубликовал как доказанный другой факт, который оказался неверным. Пять лет спустя после публикации соответствующей статьи другой великий математик, Нильс Хенрик Абель, указал на эту ошибку, приведя контрпример. Вам может показаться, что речь здесь идёт о каких-то тонких и отстранённых материях, почти философских, но на самом деле нет — речь идёт о вполне конкретных математических объектах (функциональных рядах) и, следуя буква в букву неправильной теореме, вполне можно прийти к весьма конкретным неправильным выводам. Например, что 1=0. «Научная дисциплина является настолько научной, насколько много в ней математики» — эти слова Канта именно о строгости и формализме. Не об изобилии цифр.

Со вторым чуть сложнее; зато тут можно закончить болтовню и перейти к конкретике. В доказательствах мы главным образом следовали простому плану:
  • Выписать всё, что дано, с расшифровкой всех важных определений. Важность определений определяется в основном интуитивно; если вы не уверены, выписывайте всё, что знаете.
  • Выписать всё, что требуется доказать. Опять-таки, с расшифровкой. Мы должны знать, куда идти.
  • Прийти от первого ко второму последовательностью загадочных трюков. На этом остановимся ещё подробнее.

Я не раз в тексте упоминал некоторые «фокусы»; это была фигура речи. Мне кажется, это довольно забавное название для приёмов, которые трудно придумать, но легко запомнить. Ну в самом деле, давайте разберём на примере доказательства непрерывности произведения.

Например, вот такой переход:
|f^2(x)−f^2(x_0)|=|f(x)−f(x_0)|⋅|f(x)+f(x_0)| .
Все знают формулу разности квадратов (по крайней мере, должны знать). Весь фокус здесь лишь в том, чтобы догадаться её применить — догадаться, что это может быть полезно. Зато теперь, если у вас есть информация про разность величин, а нужно исследовать разность их квадратов, вы знаете, что делать. Запомнить этот приём имеет смысл независимо от доказательства непрерывности произведения — он пригодится вам не раз.

Дальше, переход
\begin{array}{l}|f(x)+f(x_0)|=|f(x)−f(x_0)+2f(x_0)|\\[4mm] \hspace{2cm}≤ |f(x)−f(x_0)| + 2|f(x_0)| .\end{array}
Является «фокусом» в том смысле, что даёт лаконичный подход к доказательству интуитивно понятного. Интуитивно ясно, что если x близко к x_0 и функция f непрерывна, то f(x) близко к f(x_0) и сумма этих двух величин близка к 2f(x_0). Если же вы теперь попытаетесь это строго доказать, вы, вероятно, заметите, что короче, чем в предыдущей выкладке, не получится. Первый приём — добавить и вычесть одну и ту же величину — встретится вам в математике ещё не раз и ценен сам по себе. Второй приём — неравенство для модуля суммы |a+b|≤|a|+|b| — тоже используется повсеместно. А там, где его нельзя использовать, математики придумывают операции, «похожие» на взятие модуля, чтобы можно было.

Вообще, если вы будете стараться видеть за формулами идеи, те самые «интуитивно понятные» переходы (а я очень стараюсь их здесь раскрывать), доказательства будут даваться вам гораздо легче.

Далее, чудесная формула
f⋅ g = (1) ⁄ (2)\Big((f+g)^2−f^2−g^2\Big) ,
позволившая свести всё к квадратам. Пожалуй, она и есть та самая центральная идея доказательства, которую нужно запомнить. Запомнив этот переход, вы сможете перейти к доказательству более простого факта — непрерывности квадрата непрерывной функции — и проделать его, используя элементарные приёмы, которые я описал. Впрочем, следовать приведённому доказательству вовсе не обязательно. Можно попытаться придумать своё, без использования этой идеи (это не критично, она просто сэкономила нам время… наверное). Например, давайте попытаемся «в лоб» расписать неравенство
≤ft|f(x)⋅ g(x)−f(x_0)⋅ g(x_0)\right|<ε при |x−x_0|<δ_p(ε) .
Ну что тут можно сделать? Разности квадратов никакой уже нет, неравенство с модулями использовать бессмысленно. Остаётся что-нибудь добавить и вычесть. Что именно? f(x)g(x) бессмысленно, f(x_0)g(x_0) бессмысленно. Но это нечто всё ещё должно иметь отношение к f, g, x и x_0. Ну так давайте добавим и вычтем что-нибудь смешанное! f(x)g(x_0), например:
\begin{array}{c}\hspace{−5.5cm}≤ft|f(x)⋅ g(x)−f(x_0)⋅ g(x_0)\right|=\\[4mm] ≤ft|f(x)g(x)−f(x)g(x_0)+f(x)g(x_0)−f(x_0)g(x_0)\right| .\end{array}
Попробуем повыносить что можно за скобки:
\begin{array}{c}\hspace{−4cm}≤ft|f(x)⋅ g(x)−f(x_0)⋅ g(x_0)\right|=\\[4mm] ≤ft|f(x)\big(g(x)−g(x_0)\big)+\big(f(x)−f(x_0)\big)g(x_0)\right| .\end{array}
Теперь налицо уже некоторая сумма, давайте применим долгожданное неравенство:
\begin{array}{c}\hspace{−4cm}≤ft|f(x)⋅ g(x)−f(x_0)⋅ g(x_0)\right|≤\\[4mm] ≤ft|f(x)\big(g(x)−g(x_0)\big)\right|+≤ft|\big(f(x)−f(x_0)\big)g(x_0)\right|=\\[4mm] |f(x)|⋅|g(x)−g(x_0)|+|f(x)−f(x_0)|⋅|g(x_0)| .\end{array}
И вот у нас уже есть нечто, с чем интуитивно понятно, что делать. Модули с разностями меньше сколь угодно малых ε по условию; величина |g(x_0)| фиксирована, а |f(x)| близка к фиксированной |f(x_0)| (и «фокусом», описанным выше, можно это доказать). Все «почти фиксированные» величины умножаются на сколь угодно малые, и лишь потом складываются, а значит, сделать и всё выражение в правой части меньше сколь угодно малого ε не будет проблемой. Ну а тут уже идёт чисто техническая часть. Мы решаем, что проще всего сделать оба слагаемых меньше ε⁄2 (чтобы сумма была меньше ε), подбираем соответствующим образом δ_f и δ_g, берём δ_{f⋅ g} равным наименьшему из них и получаем отличное доказательство, которое ничем не хуже приведённого ранее. Непрерывность квадратов вытекает из доказанного утверждения (то, что мы указывали её отдельно, было избыточно), проблема решена, свойство непрерывных функций доказано. Успех.

Конечно, на деле проворачивать такие вещи удаётся не сразу, и выработка хорошей математической интуиции требует многих лет опыта. Я лишь хотел показать, что нет в этом никакой мистики и чёрной магии.

2.2. Непрерывность композиции функций

Попутно с объяснением ещё одного свойства непрерывных функций мы узнаем об одной важной операции над функциями — композиции функций.

Пусть есть две функции f и g, и так случилось, что R(f)⊆ D(g), то есть все значения f лежат в области определения g. Это значит, что мы имеем право подставлять величины f(x) в качестве аргументов g, то есть вычислить g(f(x)) для всевозможных x∈ D(f). Функция s: s(x)=g(f(x)) с областью определения, совпадающей с D(f), и областью значения, совпадающей (разумеется) с R(g), называется композицией, или суперпозицией функций g и f и обозначается g\circ f.

Можно приводить разные примеры композиции функций. Например, яркие и громоздкие:
s(x)=\cos(\sin x)=(\cos\circ\sin)(x) .
Или полезные, но неприметные:
s(x)=\sin^2x=(f\circ\sin)(x), где f(x)=x^2 .
Композицию можно проводить несколько раз подряд, при этом она ассоциативна, то есть от расстановки скобок в выражении f_1\circ f_2\circ…\circ f_n итог не изменяется:
s(x)=√[3]{\cos(\sin x)}=(f\circ(\cos\circ\sin))(x)=((f\circ\cos)\circ\sin)(x) ,
где f(x)=√[3]{x}. Это значит, что при суперпозиции нескольких функций подряд скобки можно опускать:
s(x)=√[3]{\cos(\sin x)}=(f\circ\cos\circ\sin)(x), где f(x)=√[3]{x} .
С другой стороны суперпозиция, конечно же, не коммутативна, то есть от перемены мест «множителей» местами результат может измениться:
(\cos\circ\exp)(x)=\cos e^x\not\equiv e^{\cos x}=(\exp\circ\cos)(x) .

Что же касается непрерывности композиции непрерывных функций, то имеет место следующий факт.

Утверждение. Пусть f непрерывна в точке x_0 и f(x_0)=y_0, и g непрерывна в точке y_0. Тогда суперпозиция s=g\circ f этих двух функций непрерывна в точке x_0.

Доказательство. Итак, дано: для любого сколь угодно малого ε>0 можно подобрать такие δ_f=δ_f(ε), δ_g=δ_g(ε), что
|f(x)−f(x_0)|<ε при |x−x_0|<δ_f(ε) и \hphantom{.}
|g(y) − g(y_0)|<ε при |y−y_0|<δ_g(ε).\hphantom{ и }
Требуется для любого сколь угодно малого ε>0 подобрать такое δ_s=δ_s(ε), чтобы выполнялось условие
|g(f(x))−g(f(x_0))|<ε при |x−x_0|<δ_s .
Интуитивный план доказательства: f непрерывна в точке x_0 — значит, y=f(x) и y_0=f(x_0) близки; g непрерывна в точке y_0 — значит, g(y)=g(f(x)) и g(y_0)=g(f(x_0)) тоже близки. Формально же это будет звучать так.

Положим δ_s(ε)=δ_f(δ_g(ε)), то есть возьмём δ_s=δ_f\circδ_g. Тогда при |x−x_0|<δ_s имеем
|f(x)−f(x_0)|<δ_g(ε) ;
стало быть, |y−y_0|<δ_g и
|g(f(x))−g(f(x_0))|=|g(y)−g(y_0)|<ε .
Доказано.

2.3. Непрерывность максимума и минимума

Давайте здесь же до кучи разберём ещё один пример операции над функциями, да ещё и сохраняющей непрерывность — взятие максимума/минимума из двух функций. (Если вы сыты по горло ε-δ-доказательствами, можете пропустить этот параграф; а лучше — докажите основные утверждения самостоятельно, это будет крайне полезная практика.)

Итак, (поточечным) максимумом из двух функций f и g называется функция, обозначаемая M=\max{f,g} и определяемая равенством
M(x)=\max{f(x), g(x)} ;
соответственно, (поточечным) минимумом из двух функций f и g называется функция, обозначаемая m=\min{f,g} и определяемая равенством
m(x)=\min{f(x), g(x)} .
То есть мы просто поточечно берём либо максимум, либо минимум из значений фукнций. Областью определения функций \max{f,g} и \min{f,g} по-прежнему будем считать пересечение областей определения f и g:
D(M)=D(m)=D(f)∩ D(g) .

Внимание! Не путайте это с понятием максимума функции, о котором пойдёт речь дальше.

Геометрически это можно понять так. Вот мы берём две функции f и g и строим график. На графике у нас будут две кривые линии, где-то пересекающиеся, где-то отдаляющиеся. Тогда графиком максимума из этих функций будет кривая, составленная из «верхних кусочков» этих двух кривых, а графиком минимума — из «нижних кусочков». Проще понять на примере; на графике ниже вы легко найдёте то, что было графиком f(x)=\sin x и то, что было графиком g(x)=(|x|) ⁄ (2)−2; красным выделен максимум из этих двух функций, а зелёным — минимум:

Операция взятия максимума ассоциативна и коммутативна, то есть если есть три функции f, g, h, то максимумы можно брать в абсолютно любом порядке:
\max{f,g}=\max{g,f} и
\max{\max{f,g},h}=\max{f,\max{g,h}} .
Так что если нам нужно брать максимум из нескольких функций, мы можем сразу без скобок писать \max{f,g,h}. Кстати, в этом случае наши геометрические рассуждения никуда не деваются, а даже становятся нагляднее:

Как видно, здесь мы добавили в максимум функцию h(x)=(x⁄3)^3.

Итак, графики подсказывают нам, что максимум из непрерывных функций непрерывен. Ну давайте докажем, что так и есть.

Утверждение. Пусть функции f и g обе непрерывны в точке x_0. Тогда их поточечные максимум M=\max{f,g} и минимум m=\min{f,g} тоже непременно непрерывны в этой точке.

Доказательство. Давайте сперва докажем для максимума. Дано: для любого сколь угодно малого ε>0 можно подобрать такие δ_f=δ_f(ε), δ_g=δ_g(ε), что
|f(x)−f(x_0)|<ε при |x−x_0|<δ_f(ε) и \hphantom{.}
|g(x) − g(x_0)|<ε при |x−x_0|<δ_g(ε).\hphantom{ и }
Требуется для любого сколь угодно малого ε>0 подобрать такое δ_M=δ_M(ε), чтобы выполнялось условие
|\max{f(x),g(x)} − \max{f(x_0),g(x_0)}|<ε
при |x−x_0|<δ_M.

Кажется, здесь уже одними «фокусами» не отделаешься, так что придётся включить логику.

Давайте отталкиваться от того, что у нас в задаче фиксировано. ε у нас произвольное положительное, x произвольное близкое к x_0… Фиксированным остаётся только x_0 и значения функций в этой точке. Здесь возможны три варианта развития событий:
  1. f(x_0)>g(x_0), и тогда \max{f(x_0),g(x_0)}=f(x_0);
  2. f(x_0)<g(x_0), и тогда \max{f(x_0),g(x_0)}=g(x_0);
  3. f(x_0)=g(x_0), и тогда \max{f(x_0),g(x_0)}=f(x_0)=g(x_0).
Рассмотрим первый вариант. Интуитивное доказательство звучит так: раз график f выше графика g в точке x_0 и обе эти функции непрерывны, то и некоторый маленький кусочек графика f (вокруг точки x_0) выше соответствующего кусочка графика g; значит, весь максимум на этом маленьком кусочке равен f, и непрерывность максимума вытекает из непрерывности f.

Теперь формально. Обозначим разность величин f и g в точке x_0 через Δ: Δ=f(x_0)−g(x_0). Возьмём δ=\min{δ_f(Δ⁄2),δ_g(Δ⁄2)}. Это такое δ, что при |x−x_0|<δ одновременно f(x) отличается от f(x_0) не больше, чем на Δ⁄2, и g(x) также отличается от g(x_0) не больше, чем на Δ⁄2. Но поскольку f(x_0) и g(x_0) отличаются ровно на Δ, мы можем заключить, что g(x)<f(x) при |x−x_0|<δ. Вот как получить это неравенство формально: во-первых, |f(x)−f(x_0)|<Δ⁄2, то есть
−(Δ) ⁄ (2) < f(x) − f(x_0) < (Δ) ⁄ (2) ,
откуда
f(x_0) − (Δ) ⁄ (2) < f(x) < f(x_0) + (Δ) ⁄ (2) .
Во-вторых, совершенно аналогично
\begin{array}{ccl} g(x) & < & g(x_0) + (Δ) ⁄ (2) = \big(f(x_0) − Δ\big) + (Δ) ⁄ (2)\\[4mm] & = & f(x_0) − (Δ) ⁄ (2) < f(x) . \end{array}
Есть.

Итак, при |x−x_0|<δ мы имеем g(x)<f(x). Значит, при всех таких x максимум достигается на f, то есть
M(x)=\max{f(x),g(x)}=f(x) при |x−x_0|<δ .

Что ж, остаётся угадать решение. Возьмём δ_M(ε)=\min{δ,δ_f(ε)}. Очевидно, что при таком раскладе δ_M(ε)≤ δ и δ_M(ε)≤δ_f(ε). Тогда при |x−x_0|<δ_M(ε) имеем наконец
|M(x)−M(x_0)|=|f(x)−f(x_0)|<ε .
Первый переход (равенство) возможен потому, что при |x−x_0|<δ_M(ε)≤δ, как мы показали выше, M(x)=f(x); второй переход (неравенство) — потому, что при |x−x_0|<δ_M(ε)≤δ_f(ε) мы имеем |f(x)−f(x_0)|<ε благодаря непрерывности f. То есть мы подобрали δ_M так, чтобы выполнялись одновременно два условия, позволившие нам получить ответ; именно для этого нам пришлось взять наименьшее из двух дельт.

Итак, первый вариант рассмотрен. Второй вариант ему полностью аналогичен — достаточно поменять местами f и g. Остаётся третий: f(x_0)=g(x_0). (Обозначим это число через y_0: y_0=f(x_0)=g(x_0).) Вся наша аргументация с Δ рушится, потому что оно оказывается равно нулю и мы больше не можем вычислить δ_f(Δ⁄2). Но здесь, к счастью, всё проще: возьмём δ_M(ε)=\min{δ_f(ε),δ_g(ε)}, или, в терминах введённой нами в этом параграфе операции поточечного минимума, δ_M=\min{δ_f,δ_g}. Тогда при |x−x_0|<δ_M
\begin{array}{l} |\max{f(x),g(x)}−y_0|\\[2mm] \hspace{2cm}≤\max{|f(x)−y_0|, |g(x)−y_0|}<ε . \end{array}
Почему это так? Давайте посмотрим. Вот у нас есть скобка |\max{f(x),g(x)}−y_0| в какой-то точке x. Она равна либо |f(x)−y_0|, либо |g(x)−y_0|. А значит, точно не больше наибольшего из этих двух чисел! (И не меньше наименьшего, разумеется.) В свою очередь, каждое из этих чисел при |x−x_0|<δ_M(ε) меньше ε, так что и наибольшее из них, разумеется, меньше ε.

На этом возможные случаи исчерпаны, и утверждение доказано.

Хотя нет! А как же минимум? Ну, к счастью, с ним очень просто. Вариант первый — проведите рассуждения, полностью аналогичные этим, для минимума. Вариант второй — воспользуйтесь чудесным равенством
\min{f,g}=−\max{−f,−g} .
(Ну и само равенство проверьте заодно. Почему оно справедливо?)

Максимум из бесконечного числа функций
Выше мы обсудили взятие максимума из нескольких функций, выписывая всё на примере трёх. Конечно, можно пойти дальше и рассматривать максимум из произвольного количества функций:
M(x)=\max{f_1(x), f_2(x), …, f_n(x)} .
Понятно, что это не новое определение, а просто более удобная запись старого и что в глубине души
M=\max{f_1,\max{f_2,…, \max{f_{n−1},f_n}…}}} .
Раз так, то из непрерывности функций f_1,…,f_n должна вытекать непрерывность функции M, ведь мы можем поочерёдно применять наше утверждение — сначала к \max{f_{n−1},f_n}, потом к \max{f_{n−2},\max{f_{n−1},f_n}} и так далее, пока не дойдём до M. При этом число n может быть, в принципе, сколь угодно большим. Тут у самых любопытных может возникнуть вопрос: а можно ли взять максимум из бесконечного числа функций? (Не самым любопытным тоже стоит почитать, потому что тут мы снова затронем вопрос строгости.)

Одним может показаться, что, очевидно, можно (почему бы и нет?); иные могут даже воскликнуть, что почему бы ему ещё и не быть непрерывным при этом. Другие могут испугаться самого факта столкновения с бесконечностью, которого можно было избежать; наиболее прагматичные могут даже возмутиться столь бездарной тратой времени. Что ж, это повод копнуть поглубже.

Взять максимум из бесконечного числа функций действительно не проблема. Ну в самом деле, определим функцию M как
M(x)=\max{f_1(x),f_2(x),…,f_n(x),…} .
В каждой точке x штука в фигурных скобках — не что иное, как числовая последовательность; если нам повезло и она ограниченная, то максимум вроде бы можно взять. Однако, это не совсем так. Посмотрите на последовательность a_n=1−1⁄n: она ограничена сверху числом 1 и подкрадывается к нему сколь угодно близко, так что только это число может претендовать на роль максимума; однако, сама единица в этой последовательности никогда не встречается. То есть речь уже идёт о верхнем пределе последовательности. Это создаёт некоторые проблемы. Помните, как мы в доказательстве говорили, что максимум равен либо значению одной функции, либо другой? Так вот, здесь это уже не так. Ну ладно, может, доказательство можно как-то улучшить?

Оказывается, что нет. Определение-то можно: заменим максимум на супремум и получим вполне нормальное, зачастую работающее определение:
M(x)=\sup{f_1(x),f_2(x),…,f_n(x),…} .
А теперь разберёмся, почему нельзя улучшить теорему. Возьмём следующие функции:
f_n(x)=√[n]{x}, n=1,2,… .
Довольно простой пример. Старые добрые корни. Взглянем на них:

Они все чудесны и непрерывны.

Ясно видно, что каждая из этих функций больше предыдущей и, соответственно, максимум из первых n таких функций равен n-й, последней. Ясно видно и ещё кое-что: если мы будем и дальше брать такие функции, то максимум в каждой точке (кроме нуля!) будет равен единице. Это простая задачка на пределы:
\lim_{n\rightarrow∞}√[n]{x}=1 при x>0 .
Стало быть, M(x)=1 при x>0.

Ну а в точке x они все нули, значит, и максимум из них всех тоже ноль: M(0)=0. Получаем в итоге функцию
M(x)=≤ft{ \begin{array}{l} 0 при x=0;\\[2mm] 1 при x>0 . \end{array} \right.
И в точке 0 она не непрерывна.

Мораль: нельзя даже капельку менять формулировки утверждений, не подумав как следует и не доказав тщательно новый вариант.

2.4. Значения непрерывных функций

Когда мы рассуждали на тему функций в физике (типа положения машины в зависимости от времени), мы мотивировали необходимость в определении непрерывности тем, что нам нужны функции, «плавно» изменяющие своё значение. Машина, говорили мы, не может «дёргаться» в пространстве — если она попала из пункта А в пункт Б, значит, она проехала и все промежуточные пункты.

Так ли это оказалось в итоге для непрерывных функций? Вроде бы да. А формально доказать? Ну давайте попробуем.

Утверждение. Пусть функция f определена и непрерывна на отрезке [a,b] вещественной прямой; её значения на краях отрезка равны f(a) и f(b). Тогда какое бы значение c, промежуточное между f(a) и f(b), мы ни взяли, всегда найдётся такая точка отрезка x∈[a,b], что значение функции в этой точке в точности равно c: f(x)=c.

Доказательство. Что ж, начнём. Сразу предупреждаю: это доказательство потребует от нас некоторых дополнительных определений.

Так, во-первых, для определённости предположим, что f(a)<f(b). Понятно, что (ну или «убедитесь, что») противоположный случай сводится к этому. Тогда заодно имеем
f(a) < c < f(b) .
(Везде строгое неравенство, потому что окажись c равно одному из крайних значений, доказательство стало бы тривиальным.)

Определим два множества:
L = {x∈[a,b]: f(x)<c}
и
G = {x∈[a,b]: c<f(x)} .
То есть множество точек, в которых значение функции меньше заветной величины, и множество точек, в которых больше. Ясно, что L,G⊂ [a,b] и a∈ L (потому что f(a)<c), b∈ G (ибо c<f(b)). Стало быть, L и G заведомо не пусты.

Казалось бы, где-то эти множества да и должны встретиться! И именно в точке встречи величина f должна оказаться равной c! Так и будет, но не сразу.

Попробуем дать определения, которые формализуют это понятие «точки встречи». Точно ли можно, скажем, в L найти крайнюю правую точку? Или в G — крайнюю левую?

2.4.1. Верхние и нижние грани

Итак, верхней гранью множества вещественных чисел X называется любое число M, которое больше (либо равно) всех чисел, содержащихся в X:
x ≤ M для всех x∈ X .
Соответственно, точной верхней гранью, или супремумом множества вещественных чисел X называется «наиточнейшая», наименьшая из его верхних граней, то есть число M_∗ (обозначаемое \sup X) такое, что:
  1. оно больше (либо равно) всех чисел, содержащихся в X, то есть является верхней гранью;
  2. при этом если уменьшить его на сколь угодно малое ε>0, то в X найдётся число x_{ε}, которое окажется больше:
    x_{ε}>M_∗−ε ,
    то есть не существует верхней грани, которая была бы меньше M_∗.
Пример: числа 1, 2, 3, … являются верхними гранями множества X=[0,1], но только единица является его точной верхней гранью.

Совершенно аналогично можно ввести нижнюю грань и инфимум. Нижней гранью множества вещественных чисел X называется любое число m, которое меньше (либо равно) всех чисел, содержащихся в X:
m≤ x для всех x∈ X .
Соответственно, точной нижней гранью, или инфимумом множества вещественных чисел X называется наибольшая из его нижних граней, то есть число m^∗ (обозначаемое ∈f X) такое, что:
  1. оно меньше (либо равно) всех чисел, содержащихся в X, то есть является нижней гранью;
  2. при этом если увеличить его на сколь угодно малое ε>0, то в X найдётся число x_{ε}, которое окажется меньше:
    m^∗+ε>x_{ε} ,
    то есть не существует нижней грани, которая была бы больше m^∗.
Пример: числа 0, −1, −2, … являются нижними гранями всё того же множества X=[0,1], но только ноль является его точной нижней гранью.

Если откладывать точные грани множества X на вещественной прямой, то, каким бы ни было множество X, точная верхняя грань окажется самой правой точкой X, а точная нижняя — самой левой:

Всегда ли точные грани (как точки вещественной прямой) будут принадлежать соответствующему множеству X? Нет. Достаточно взглянуть на интервал (0,1). Его точной нижней и верхней гранями являются ноль и единица; это легко проверить по определению (сделайте это!), однако в самом множестве они не лежат. То есть точная верхняя грань — не обязательно максимальное число множества: максимального числа во множестве может и вовсе не быть.

И сразу следующий, не менее резонный вопрос: а всегда ли вообще существуют точные грани? Что ж, например, у всей вещественной прямой ℝ никаких граней, разумеется, нет: нельзя подобрать вещественное число, которое было бы больше либо равно (или меньше либо равно) всех остальных (как известно, никакая «бесконечность» не считается корректным вещественным числом).

Однако, при некоторых ограничениях точные грани есть. И ограничения эти достаточно просты. Ну, во-первых, очевидно, что для того, чтобы найти точную грань, нужно иметь в наличии хотя бы одну соответствующую просто грань (ну а как выбрать из граней наибольшую/наименьшую, если их нет вообще ни одной?). А во-вторых, этого оказывается и достаточно.

Давайте обозначим через m(X) и M(X) совокупности всех нижних и верхних граней множества X — из них нам нужно выбрать наибольшую нижнюю и/или наименьшую верхнюю грани. Как эти множества выглядят? Примерно так:

То есть это лучи, выходящие из точек ∈f X и \sup X. Почему? Да потому что если m — нижняя грань, то и все числа меньше m — тоже нижние грани! Если M — верхняя грань, то и все числа, большие M — тоже верхние грани! То есть достаточно одной грани, чтобы неминуемо их оказался целый луч.

Ну и ясно, что у луча на вещественной прямой всегда есть точка, из которой он выходит. Во всяком случае, это просто доказать. Если луч уходит вправо, то эта точка на самом-то деле окажется инфимумом точек луча, а если влево — супремумом. Правда, существование всех этих инфимумов и супремумов мы так и не доказали. Но мы свели общий случай, с произвольным множеством X, к частному, с лучом! Ну а для луча мы можем доказать существование супремума/инфимума (нужное подчеркнуть) просто в лоб, по определению (сделайте это!).

Итак, у этих двух лучей существуют супремум/инфимум, они будут являться точными нижней и верхней гранями множества X (проверьте), значит, у X всегда есть точная верхняя/нижняя грань, если есть хотя бы одна соответствующая просто грань (её достаточно, чтобы построить луч). Успех! (Почти. Попробуйте на досуге формализовать это доказательство настолько, чтобы в него поверил ваш преподаватель матанализа.)

2.4.2. Назад к доказательству

Ну и вернёмся к нашим непрерывным функциям. Итак, у нас есть множества
L = {x∈[a,b]: f(x)<c}
и
G = {x∈[a,b]: c<f(x)} .
Поскольку оба они лежат в отрезке [a,b], у них есть верхняя и нижняя грани — числа b и a — а значит, и точные верхняя и нижняя грани (вот тут уже Бог знает, какие именно). Обозначим одну из них: \xi=\sup L. Ясно, что \xi∈[a,b]; соответственно, функция f определена и непрерывна в точке \xi (как и во всех остальных точках отрезка [a,b]). То есть для любого ε>0 можно подобрать такое δ=δ(ε), что
|f(x)−f(\xi)|<ε при |x−\xi|<δ .

Внимание! Статья в разработке. Возможно, я дописываю её прямо сейчас. Так что ждите продолжения! (Нажмите  Поддержать проект, чтобы узнать, как можно ускорить этот процесс.)

3. Указатель

© Aleph, 2012–2016. При использовании материалов ссылка на math.siomax.ru обязательна.
Последняя редакция: , Т. Салуев.